(Image by Mysid)
In 1915, Albert Einstein introduced a new theory of gravity that he called the General Theory of Relativity. This theory has gained wide acceptance in the last 100 years, partly because its predictions more accurately match experimental evidence than the older theory of gravity developed by Isaac Newton in the late 1600's. Einstein's theory, though, also gained a reputation for being difficult to understand. In his biography of Einstein, Walter Isaacson recounts an anecdote between astrophysicist Arthur Eddington, whose experiments in 1919 provided some of the first evidence for general relativity, and scientist L. Silberstein:
"[General relativity] was a grand triumph, but not one easily understood. The skeptical Silberstein came up to Eddington and said that people believed that only three scientists in the world understood general relativity. He had been told that Eddington was one of them. The shy Quaker said nothing. 'Don't be so modest, Eddington!' said Silberstein. Replied Eddington, 'On the contrary. I'm just wondering who the third might be.'" [Walter Isaacson, "Einstein: His Life and Universe"]
It's no surprise that many people find the theory intimidating. The concepts, involving the speed of light and the curvature of spacetime, reach beyond our everyday intuition. And the details of the mathematics can be downright messy — it took Einstein years to work out the math after he had developed the basic ideas.
Nevertheless, an informal understanding of general relativity doesn't require a detailed understanding of the mathematics. We can grasp the gist of it with a few diagrams and a little imagination. In case you're feeling impatient, here's the "too long, didn't read" synopsis:
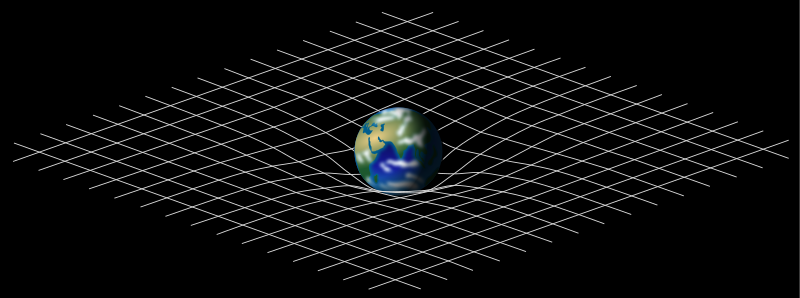
Did that synopsis go by a little too fast? Then let's walk through the explanation at a more leisurely pace, starting with the standard picture of a heavy object sitting on a mattress or a rubber sheet. You may have seen this diagram before:
(Image by Mysid)
This diagram shows a surface representing two dimensions of space, and a heavy object that causes these two dimensions to curve. The diagram conveys a simple message: massive objects cause spacetime to curve. The denser and more massive the object, the larger the curvature — the earth has a bigger impact on the shape of spacetime than a ping-pong ball does.
Although it's a good starting point, the diagram above doesn't actually explain why a curved spacetime should cause objects to fall down. You might think at first that since the massive object causes the surface to sink downwards in the diagram, that other objects would naturally "fall" downwards towards the massive object. Physicist Brian Greene demonstrates this idea by rolling balls on a curved spandex surface in this video:
But, as Greene points out, this demonstration depends on the earth already having gravity to pull the balls down, and is thus "kind of using gravity to explain gravity". It doesn't really tell us where gravity comes from in the first place, since it wouldn't work in an environment that didn't already have gravity (imagine trying it in outer space, for example, where the balls would likely just fly off the spandex surface in a straight line).
To understand how curved spacetime produces gravity from scratch, we need to go beyond just thinking about two curved dimensions of space. Spacetime is four-dimensional, with three dimensions of space and one dimension of time, and the curvature in time plays a crucial role in generating gravity. It's difficult to visualize all four dimensions being curved simultaneously, so to make things easier, let's just visualize a two-dimensional surface consisting of one dimension of space plus one dimension of time. One dimension of space isn't much — we can't visualize orbits of planets with only one dimension of space, for example. It's enough, though, to understand the simplest example of gravity: you throw a ball straight up in the air:
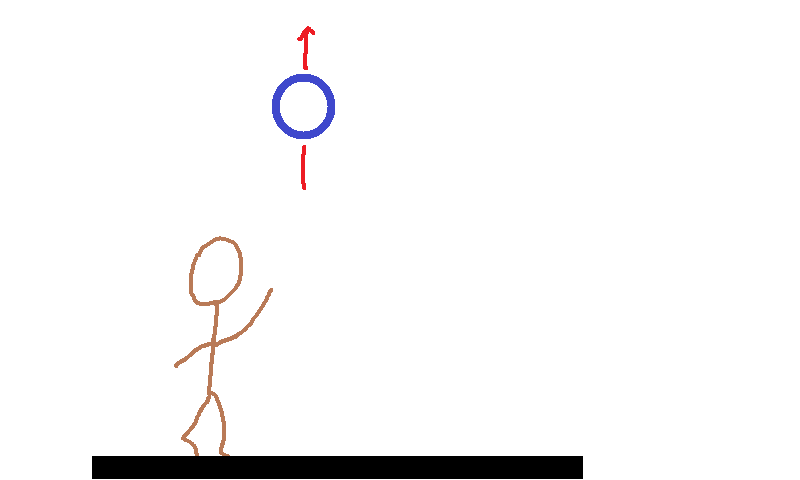
and after a few seconds the ball falls straight back down:
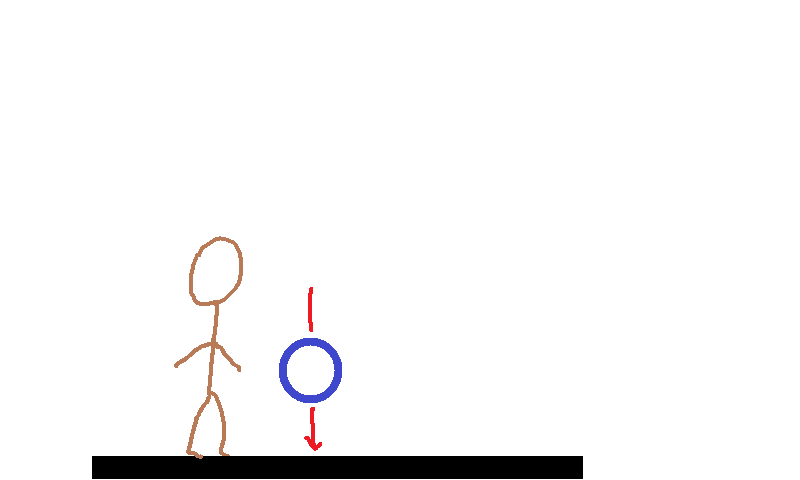
Our one dimension of space will represent the height of the ball as it rises and falls, and our task will be to explain why curved spacetime makes the ball fall down.
To do this, we first need to understand what it means for spacetime to be curved. If we look around at our everyday surroundings, things don't look particularly curved. Walls and doors look straight. Tabletops look flat. How can we even tell if spacetime is curved? Well, suppose we didn't know that the earth's surface was curved. How could we figure out the shape of the earth? We could fly high above the earth in a balloon or plane or rocket, and look down at the earth from above to see its shape. This approach won't help us learn the shape of four-dimensional spacetime, though, since there's no way to fly above spacetime itself to look at it from the outside. We live inside four-dimensional spacetime, and we can't get out. So let's think of a different strategy — is there any way to tell that a surface is curved without leaving the surface? In fact, there is.
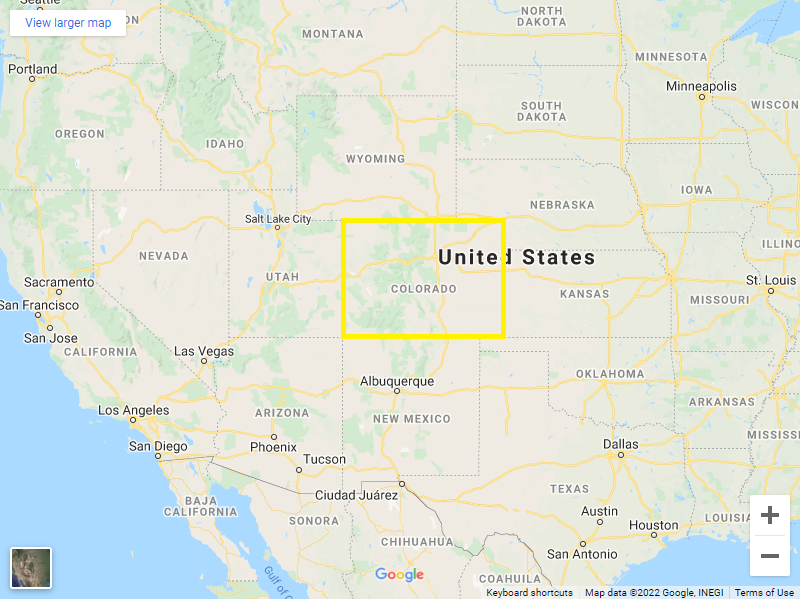
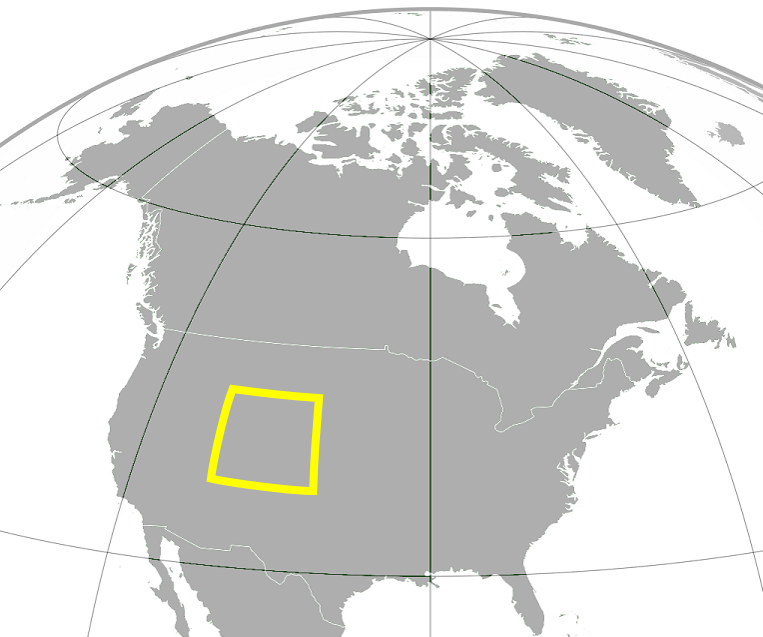
Consider the state of Colorado in the western United States. If you look at a flat map, you can see that Colorado is supposed to be shaped like a rectangle:
(Image by Google Maps)
Naturally, the rectangle has four sides. The left and right sides run straight north-south. The upper and lower sides run straight east-west. If Colorado were really shaped like a rectangle, the left and right sides would have equal length, and the upper and lower sides would have equal length. On the flat map shown above, it looks like the upper and lower sides have equal length. But in reality, they don't. The upper side is actually shorter because it is closer to the north pole than the lower side, as you can see when the state is drawn on a globe (exaggerating the state's size for clarity):
(Image by Surfer43, edited)
In fact, if Colorado stretched all the way to the north pole, it would have no upper side at all — its left and right sides would simply intersect at the north pole. As it is, Colorado's northern border is about 21 miles shorter than its southern border.
From this, we have a strategy to discover if a surface is curved: try to draw a rectangle on it, with straight lines and 90 degree angles. If we discover that opposite sides have unequal length, then the surface must be curved. Can we do this for our two-dimension spacetime surface? Absolutely! We just hang two clocks on a wall, the upper clock one meter above the lower clock:
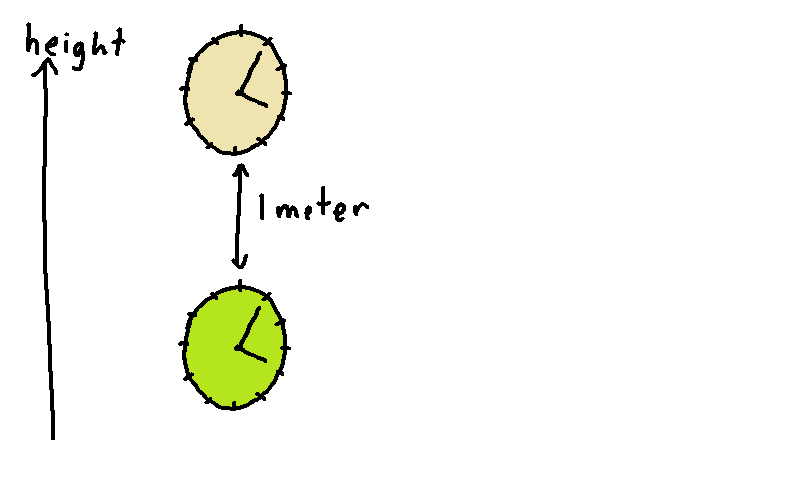
Suppose we start the clocks running on January 1, 2021. The line between the clocks, going straight up-down, will be one of the four sides of our rectangle. Now let the clocks run for a year. On January 1, 2022, we'll again have a line running straight up-down between the two clocks. This will be another side of the rectangle:
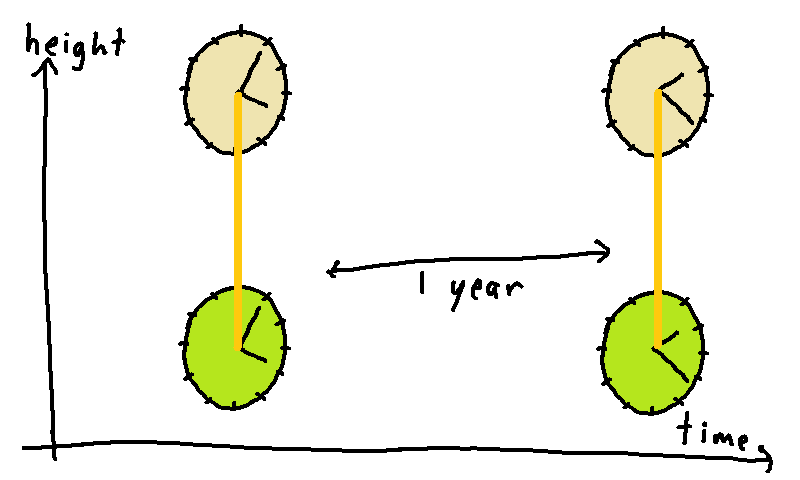
Finally, during the year, each clock will trace out a path in time, running straight from past to future. These two past-future lines will form the remaining two sides of the rectangle:
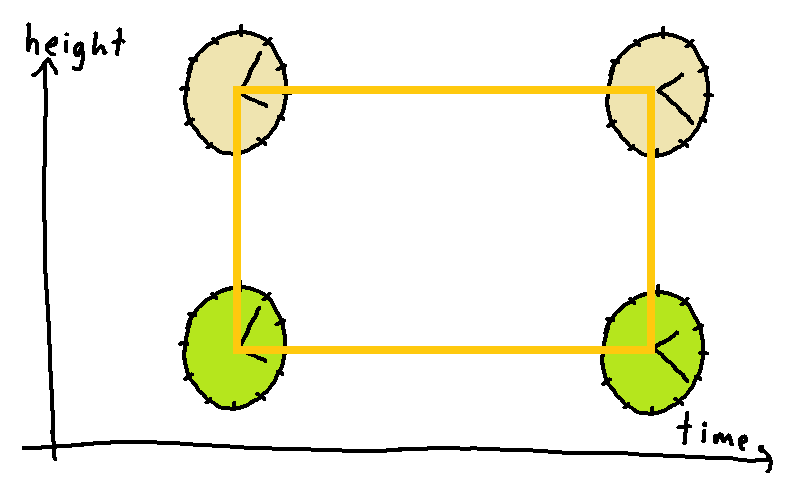
To measure the four sides of the rectangle, we need to measure both space and time: space for the left and right sides and time for the upper and lower sides. We can use meter sticks to measure space and clocks to measure time. Conveniently, since we hung two clocks on the wall, we already have the two clocks we need to measure time.
So what happens in reality when we perform these measurements? For the left and right sides, we measure exactly what anyone in Isaac Newton's time would have expected: both the left and right sides are exactly one meter long. The distance between the clocks does not change over time. For the upper and lower sides, though, we discover something astonishing. The upper and lower sides are not equal in length. Instead, the lower clock reports less time passed than the upper clock, by about 3 nanoseconds (3 billionths of a second) over the course of a year. In other words, if the upper clock shows that exactly one year has passed, the lower clock shows that one year minus about 3 nanoseconds has passed. Just as the upper and lower borders of Colorado show that the earth is curved, the upper and lower clocks show that spacetime itself is curved.
A few nanoseconds per year isn't much curvature, but it's enough for a careful experiment to detect. If you want details of an actual experiment, you can read "Optical Clocks and Relativity" by C.W. Chou, D. B. Hume, T. Rosenband, and D. J. Wineland. (Or, if you want the Hollywood rendition, you can watch a greatly exaggerated scene in the movie Interstellar where characters on the surface of a massive planet age much more slowly than characters high above the planet.) The important point is that curved spacetime is not just some abstract mathematical formula — it's real and experimentally observable, just like the curved surface of the earth is real and observable.
So what does the curvature of spacetime have to do with gravity? How could such a small amount of curvature possibly cause gravity? To understand this, let's take a deeper look at the trajectory of a ball that flies straight up:
and then falls straight back down:
To better visualize the ball's trajectory, let's plot the ball's height as a function of time on a graph, with height on the vertical axis and time on the horizontal axis. Here we plot the ball rising straight up over time:
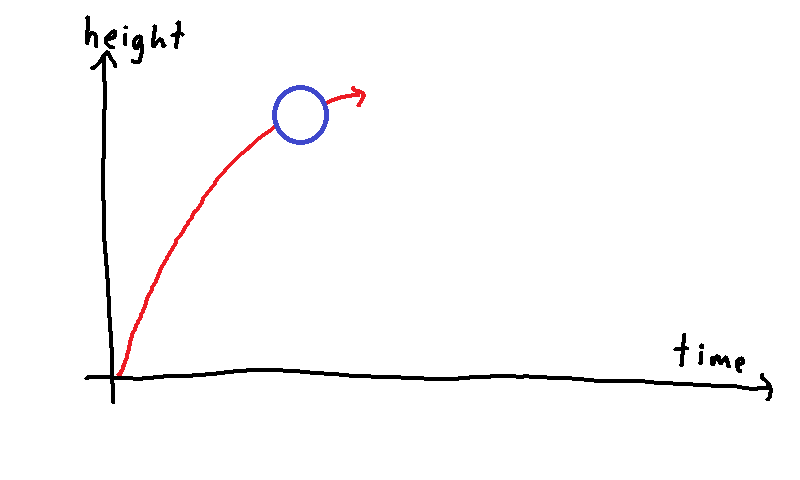
And here's the ball rising straight up and then falling straight down:
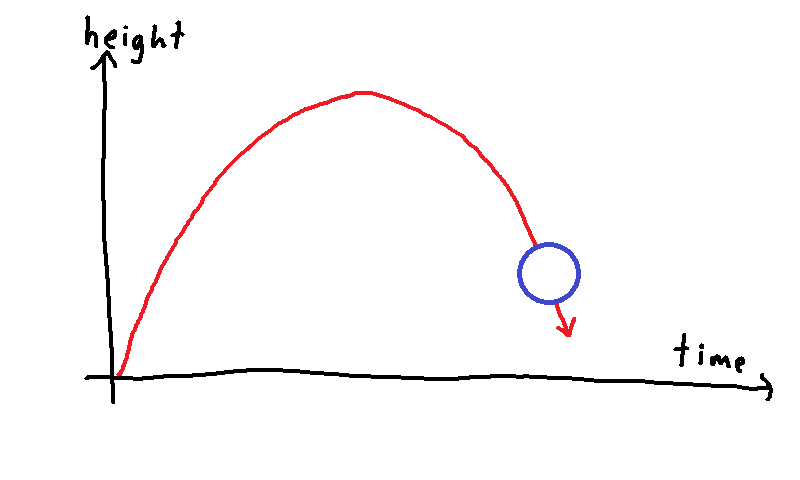
The trajectory of the ball through spacetime is not a straight line. It starts by pointing up and to the right on our graph, but then gradually curves back down and to the right. Isaac Newton would have said that this curved trajectory is the result of the force of gravity pulling the ball back towards the earth. According to Newton's first law, if there were no force acting on the object, then the object's trajectory would be a straight line ("A body continues in its state of rest, or in uniform motion in a straight line, unless acted upon by a force."). And a straight line is the straightest, shortest trajectory an object can take through flat spacetime. But spacetime isn't actually flat! And you can't make a straight line through the curved surface of spacetime. (Try drawing a 10000 mile long straight line on the curved surface of the earth. It won't be straight — a straight line would shoot off the surface into space.) So what are we to do with Newton's first law?
It turns out we can still salvage Newton's first law even in curved spacetime. Instead of saying that an object with no force travels in an exact straight line through spacetime, we'll say that the object travels in the straightest, shortest path it can. (Such a path is called a "geodesic".) We can understand what such a straightest, shortest trajectory looks like by making an analogy to the trajectory of an airplane over the surface of the earth. In this analogy, we'll look at the straightest, shortest path than an airplane can take over the surface of the earth.
[Keep in mind that this is just an analogy; the curvature of the two-dimensional surface of the earth is not the same thing as the curvature of four-dimensional spacetime. You could have one without the other: if the earth were flat but massive, the earth's surface wouldn't be curved but the earth's mass would still cause spacetime to curve near the earth. Likewise, if the earth were spherical but massless, then the earth's surface would be curved but the earth would not cause spacetime to curve.]
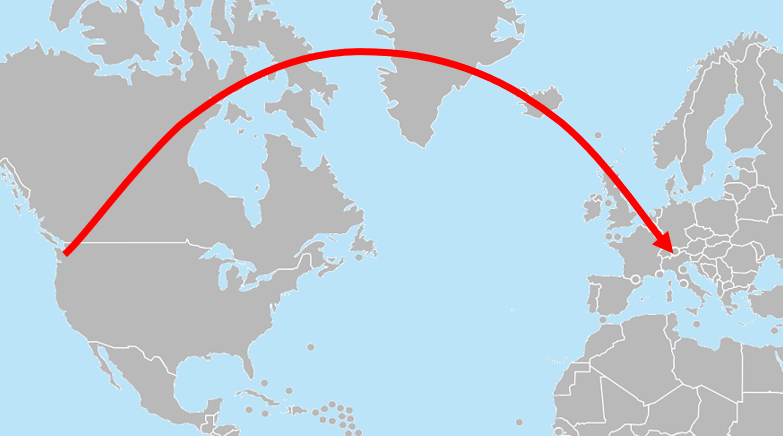
Suppose that an airplane wants to take the shortest-distance path from Seattle to Zurich. Both cities are at a latitude of about 47 degrees north, but the plane would not fly straight east at a constant 47 degree latitude. Instead, it would fly a "great circle route" that first heads north-east, then east, then south-east:
(Image by Geordie Bosanko, edited)
When projected onto a flat map, as in the picture shown above, the trajectory looks overly curved. It looks like the pilot is continuously steering slightly to right in order to gradually turn the plane's direction from north-east to east to south-east over the course of the flight. However, this is an illusion caused by the projection of the earth's curved surface onto a flat map. In reality, the pilot is actually flying the straightest possible path from Seattle to Zurich, steering neither left nor right, which we can see if we look at the flight straight down from above the earth:
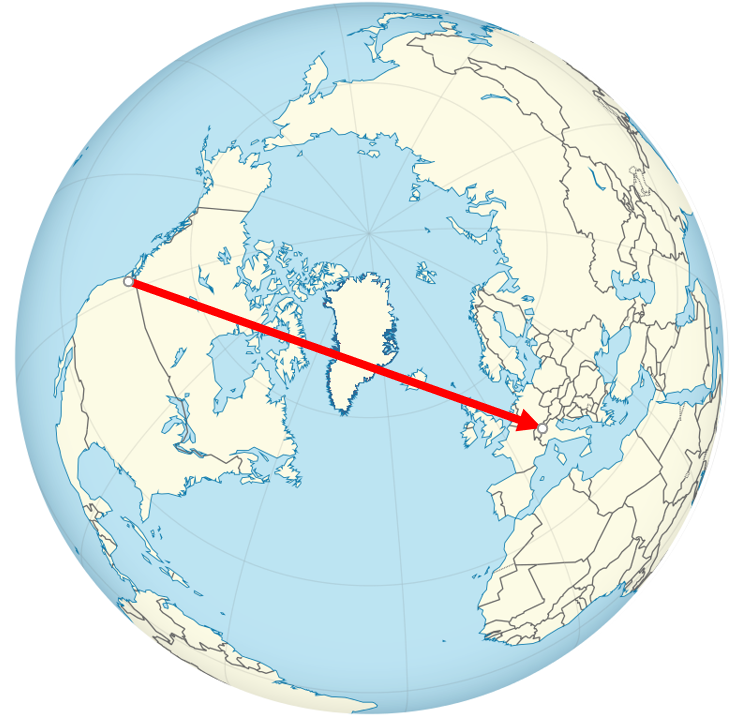(Image by TUBS, edited)
Let's go back to the picture of the flight on a flat map, though. You might have noticed that the plane's path across the flat map looks a lot like the graph of the ball rising and falling over time:
(Image by Geordie Bosanko, edited)
The two images have different axes: the flight map shows east-west on the horizontal axis and north-south on the vertical axis, while the ball trajectory shows time (not space) on the horizontal axis and height on the vertical axis. Yet both images appear to show similar curved paths that rise and then fall again. The similarity between these two figures is not a coincidence. We've already seen that for the airplane's great circle route, the overly curved path is an illusion; the path is really the straightest path possible over the curved surface of the earth. Now we come to the essence of Einstein's theory: the trajectory of the ball is actually the straightest, shortest possible path through curved spacetime. There's no force acting on the ball — gravity is not a force in Einstein's theory — so the ball takes the straightest, shortest path through curved spacetime, just as our salvaged version of Newton's first law says it should. When we project this path onto a flat graph, as in the figure above, it looks overly curved, as if there were a force acting on it. But this apparent force is an illusion, just as the airplane pilot apparently steering to the right is an illusion.
[Note that spacetime has a different shape than the surface of the earth does, although the underlying idea is the same in both cases; see the bonus section below if you're interested in more details about the shape of spacetime and a slightly more careful definition of a straightest, shortest path through spacetime.]
In contrast to an airplane taking a great circle route, an airplane that traveled directly east at a constant 47 degrees latitude would not be taking the straightest, shortest path from Seattle to Zurich, but would instead be taking a longer and more curved path, where the pilot actually steers slightly to the left throughout the journey. Similarly, a ball sitting on a table at a constant height, rather than falling, is not taking the straightest, shortest path through spacetime, but instead is being forced (by the force of the table pushing up on the ball) to take a longer, less straight path through curved spacetime. In other words, in Newton's theory of gravity, objects at rest naturally tend to stay in one place, and Newton had to add an extra force (the force of gravity) to make things fall in his theory. When spacetime is curved, though, gravity comes for free — free-fall is the default, natural, straightest possible trajectory of an object traveling via pure inertia — and you need to have a force if you want to stop something from falling.
Now, in case you're confused, this is a good time for a reminder that Einstein's theory talks about curvature in spacetime, not in space. The rising and falling ball takes the straightest, shortest route through spacetime. It does not take the shortest path through space! (If the ball took the shortest path through space, it would not go anywhere — it would just stay in one place and travel a total distance of zero meters. This is clearly not what happens as the ball rises and falls!) But even if we remember that we're talking about spacetime, you may still feel a little uneasy. We said that spacetime around the earth is curved by only a tiny amount. Gravity, on the other hand, does not seem like a tiny phenomenon to us. The trajectory that the ball takes through spacetime looks curved by a lot, not just a little:
How curved the ball's path looks, though, depends on how we draw the graph. If we make the horizontal axis shorter relative to the vertical axis, the path looks more sharply curved:
If we make the horizontal axis longer, the path looks more gently curved:
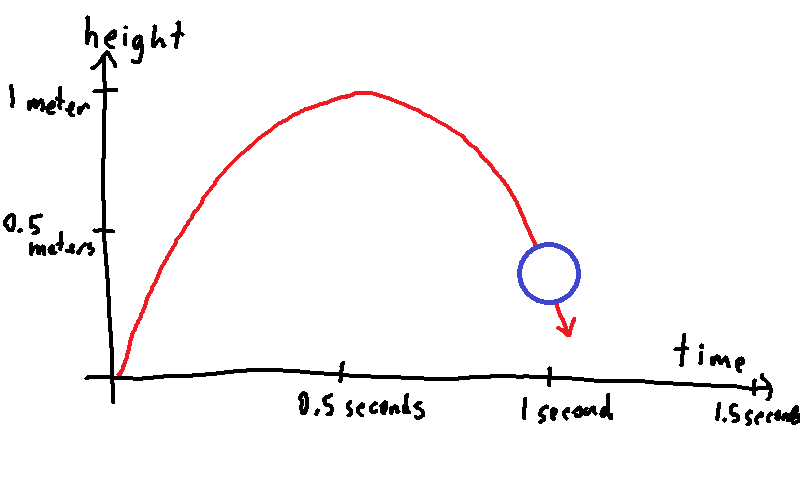
If we want see the right shape of the path, we need to choose the scale of the horizontal axis and vertical axis properly. Ideally, we should choose the same units for both axes: if one axis is measured in meters, then the other axis should also be in meters, not millimeters or kilometers. It's not obvious how to do this for our spacetime graph, though, since one axis shows distance and one axis shows time. For example, suppose that our ball takes about one second to rise one meter and fall again:
How can we use the same unit to represent both one meter of distance and one second of time? To do this, we'd need some sort of conversion between distance and time. This is actually possible. Consider how we convert distances. If the distance between two towns is 5 kilometers, we can convert that to 5000 meters by multiplying 5 kilometers by a conversion factor of 1000 meters per kilometer. If we wanted to convert one second to some number of meters, we'd need to multiply one second by a conversion factor of some number of meters per second.
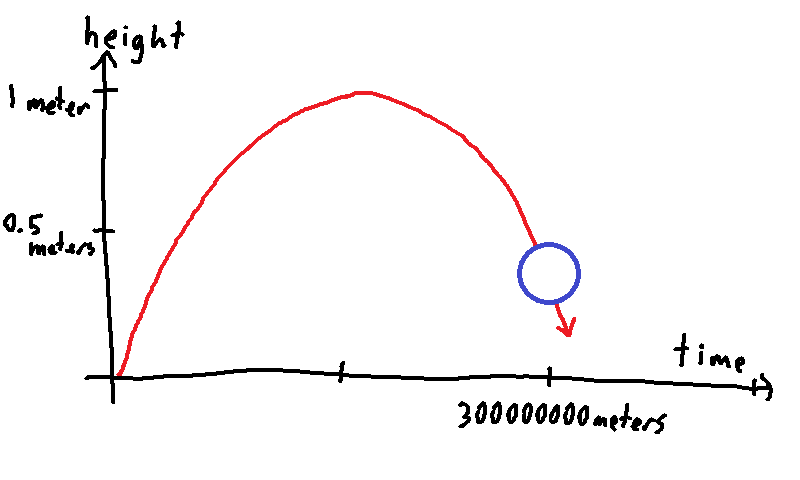
Notice that "some number of meters per second" describes a speed — we measure speed in meters per second (or miles per hour, kilometers per hour, etc.). If you've heard anything about Einstein's theory of relativity, you've probably heard that one speed in particular plays a central role: the speed of light. In Einstein's theory, the speed of light is the conversion factor between time and distance. Of course, light goes very, very fast, traveling about 300 million meters each second. So if we convert one second to meters, we multiply by about 300 million meters per second, resulting in a distance of about 300 million meters. This is a huge distance through time, especially compared to the measly one meter that the ball rises and falls in space:
In other words, from the perspective of relativity, the ball travels far more through time than through space. If we wanted to capture the scale of the ball's trip through time in our graph, we'd have to stretch the horizontal axis out 300 million times longer than the vertical axis. This is not easy to draw, but suppose we just stretch it out 30 times. If you scroll the image below to the right, you can see that the path on the graph barely looks curved at all when the horizontal axis is stretched 30 times:
You can now imagine how straight the line would look if the horizontal axis were stretched by a factor of 300 million. On this scale, the curvature in the path is tiny, and this tiny curvature in the path can easily be caused by a tiny curvature in the shape of spacetime itself.
In fact, if we measure the curvature of spacetime at the earth's surface and we know the speed of light, we can calculate how fast objects should fall. The result of this calculation indeed matches how fast we observe objects falling. Not only that, the calculations from Einstein's theory of gravity are actually more accurate than Newton's theory of gravity. For example, it was known in the late 19th century that Newton's theory of gravity didn't quite predict the orbit of the planet Mercury accurately — it was close, but off by a little, prompting some 19th-century astronomers to hypothesize an extra planet named "Vulcan" to explain the discrepancy between Newton's theory and experimental observations. Einstein's theory, by contrast, gets Mercury's orbit exactly right as far as we've been able to measure, and the idea of planet Vulcan has been left in the garbage can of history.
Einstein's theory also makes many other predictions that have been experimentally confirmed. It predicts that gravity will bend the trajectory of light (light has to travel on a curved trajectory through curved spacetime, just like everything else). It predicts that light's wavelength will get stretched out ("redshifted") as the light travels away from a massive object. It predicts the existence of gravitational waves, which don't exist in Newton's theory of gravity. All of these predications have been experimentally confirmed.
Scientists are still working on reconciling Einstein's theory of gravity with quantum mechanics. They've already successfully combined quantum mechanics with Einstein's earlier theory of "special relativity" (the basic framework of relativity, without gravity), and this successful combination is the basis for the "standard model" of particle physics that describes the force of electromagnetism, the strong nuclear force, and the weak nuclear force. Adding gravity directly to the standard model, though, runs into some mathematical difficulties, and it remains to be seen how to combine quantum mechanics and gravity together in a single mathematically harmonious theory; see this video by physicist Sabine Hossenfelder for an overview:
If you're interested in slightly more technical presentations of Einstein's theory, along with some beautiful related ideas like the "equivalence principle", the physicist Sean Carroll has a presentation of general relativity:
and the physicist Leonard Susskind has a series of lectures on general relativity:
There are also many informal explanations of general relativity on YouTube; Veritasium's explanation is a particularly nice one:
We've said so far that spacetime is curved and that the curvature results in what we perceive as gravity. We've also said that spacetime is only curved a tiny amount near the earth. But what exactly is curved spacetime shaped like? It's not shaped like any object that's familiar to us in our everyday experience. In fact, spacetime not only forms an unfamiliar shape, but uses an unfamiliar geometry, with different rules for calculating distances than we're used to. It's not easy to visualize the curved shape that spacetime makes, but we can at least make a rough attempt. We'll limit ourselves to visualizing the slight curvature that the earth forms on spacetime rather than visualizing something more wildly curved like a black hole. As before, it's easiest to look at just a two-dimensional spacetime surface consisting of one dimension of space (which, as before, we'll choose to be the height from the earth's surface) and one dimension of time.
Warning: this section involves a little math.
As a warmup exercise, consider visualizing something easier: the spherical shape of the earth's surface. Obviously, we know what this looks like in our 3-dimensional world from our experience looking at other spherical surfaces (globes, beach balls, etc.). Let's visualize it in just 2 dimensions, though, by flattening the spherical surface so we can represent it on a flat page. In order to flatten it, we need to either stretch it or tear it or both. Let's avoid stretching it very much and instead tear it into multiple sections with gaps between them, as can be seen in the following projection of the earth's surface:
(Image by Strebe)
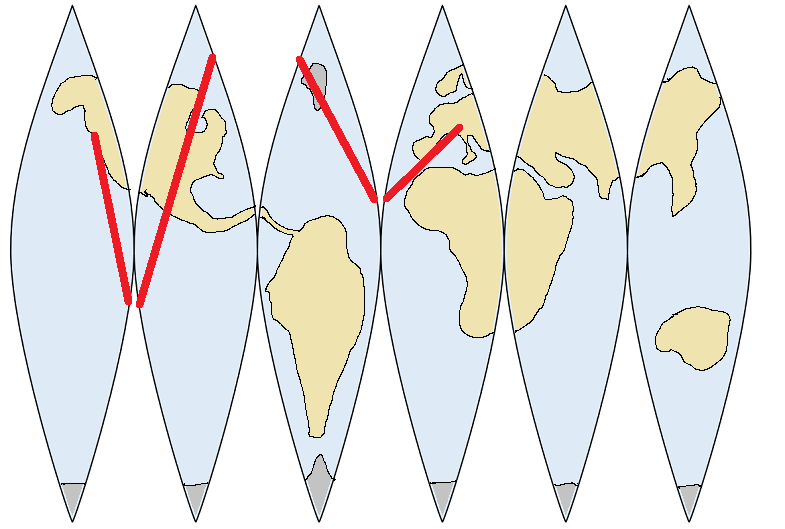
In fact, let's tear it into a lot of thin sections:
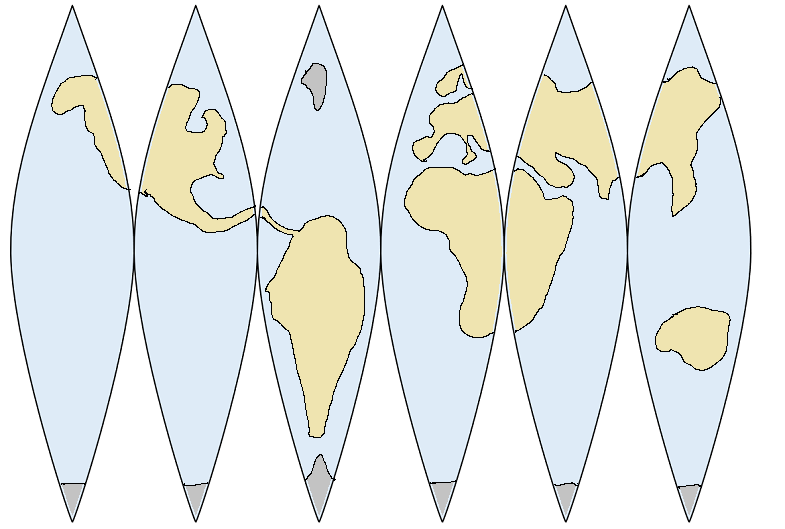
You can see that the gaps between the sections are larger near the poles, and there's no gap at all at the equator. Therefore, constant-latitude paths around the world are longer near the equator than at the poles (it's shorter to travel around the world by circling near a pole than by going all the way around the equator):
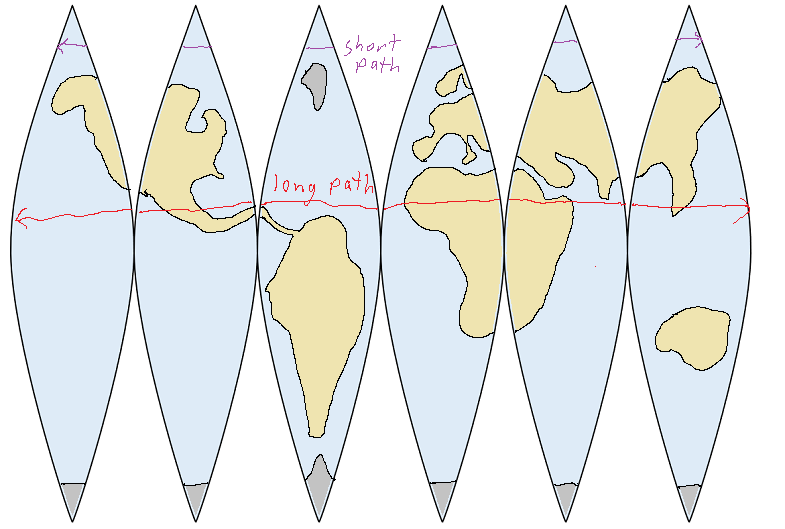
Let's draw various routes from Seattle to Zurich on the map:
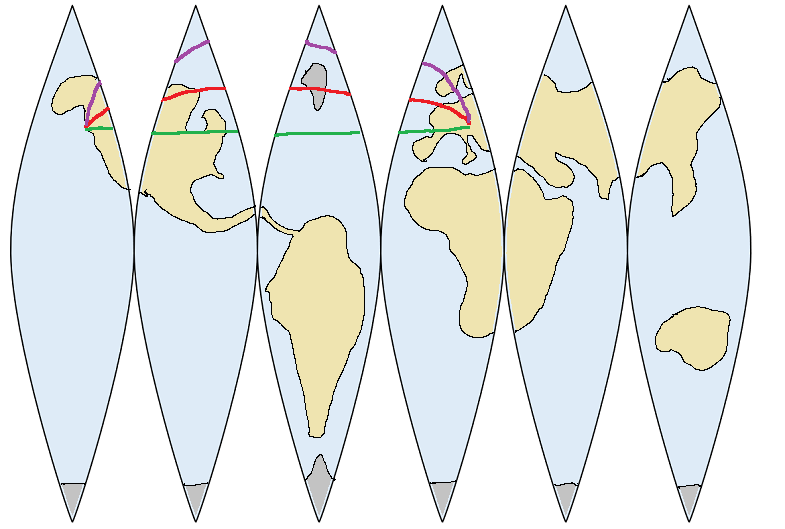
The middle route is roughly a great circle route. This is shorter than the "straight east" route because it travels more through higher latitudes where there are bigger gaps and therefore less east-west space to cover. In fact, a flight could go even further north, near the north pole, as shown in the northernmost trajectory above, which saves even more east-west travel, but costs much more in north-south travel. In the end, the shortest route (the great circle route) strikes a balance between minimizing east-west travel and minimizing north-south travel.
To show that one route is shorter than another, we have to measure the distance along each route. To make this easier, let's break the routes into short straight-line segments and pretend that each short segment travels over a completely flat surface:
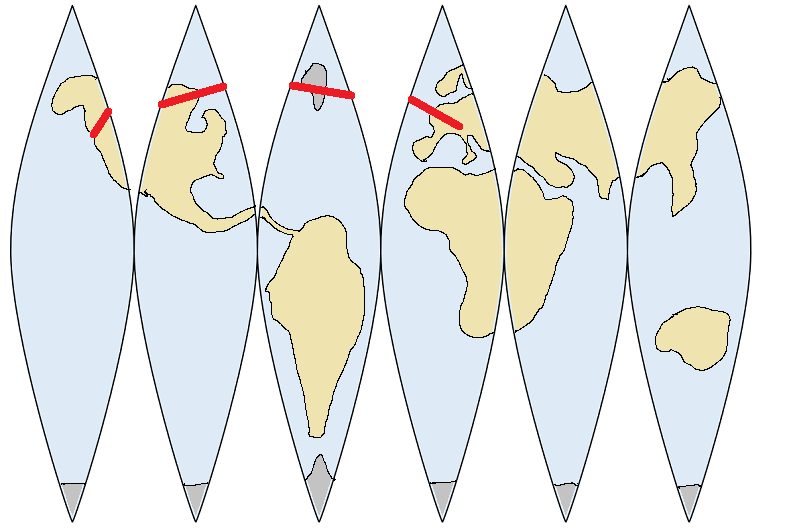
We just need to add up the lengths of all the straight-line short segments to get the approximate total distance of a route. To measure each short segment, we could just use a ruler. However, while this will work for measuring segments on the earth's surface, it unfortunately won't work for measuring distances in the unusual geometry of spacetime.
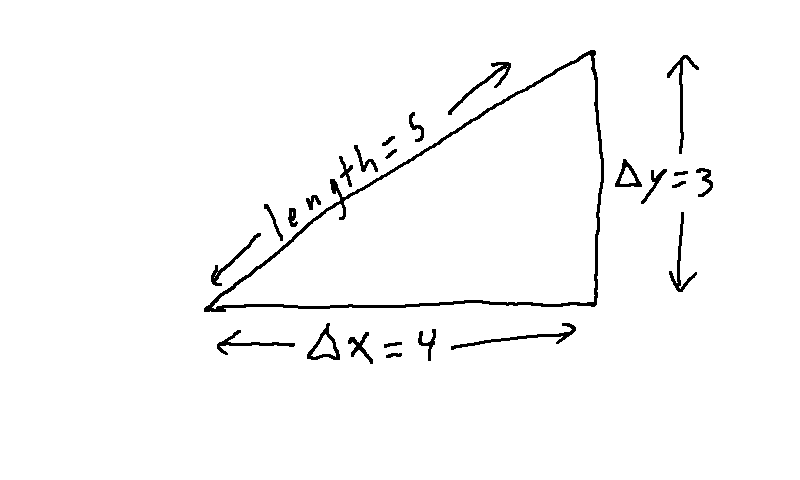
So to prepare for measuring spacetime, instead of using a ruler, let's use the Pythagorean theorem to calculate the length of each short segment. The Pythagorean theorem says that if a diagonal line covers some horizontal distance Δx and some vertical distance Δy, then the square of the length of the diagonal line equals the square of Δx plus the square of Δy:
length2 = (Δx)2 + (Δy)2.
For example, if Δx = 4 and Δy = 3, then the length of the diagonal line is 5, because 5 squared (25) equals 4 squared (16) plus 3 squared (9):
From this, we can formalize something that intuition already tells us: if we increase Δx, the length of the diagonal increases, and if we increase Δy, the length of the diagonal increases. So if we want to minimize the distance along a route, we want to keep both the Δx (the east-west distance) and Δy (the north-south distance) of each segment small. We wouldn't want, for example, a route that made huge north-south trips back and forth, as this would result in longer segments and an overall longer route:
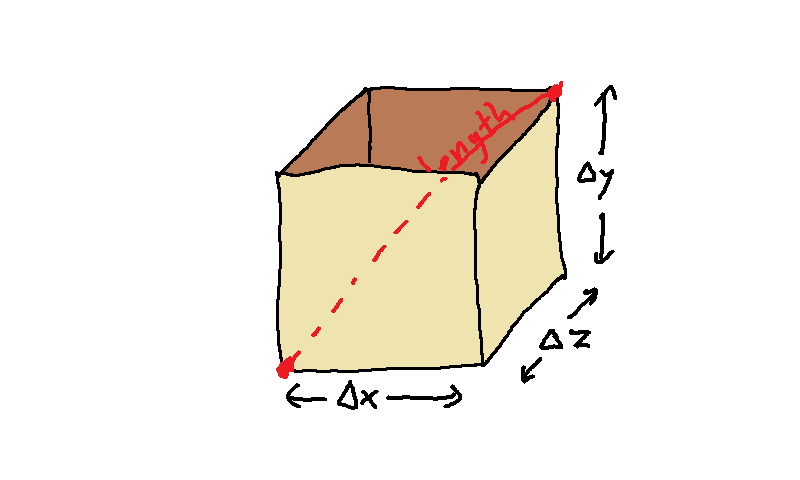
The Pythagorean theorem extends to more than two dimensions. Suppose we want to measure the diagonal of a box, going from one corner to the far opposite corner, and the box has width Δx, height Δy, and depth Δz. The square of the length of the diagonal is the sum of the squares of all three sides, (Δx)2 + (Δy)2 + (Δz)2:
Now consider the Pythagorean theorem for 4-dimensional spacetime, with dimensions x, y, z, and t (for time). You might guess, based on the 2-dimensional and 3-dimensional spatial Pythagorean theorems, that the square of the length is the sum of the squares of Δx, Δy, Δz, and Δt: (Δx)2 + (Δy)2 + (Δz)2 + (Δt)2. However, the formula in relativity is slightly different and unfamiliar — we actually subtract the square of Δt rather than adding:
(Δx)2 + (Δy)2 + (Δz)2 - (Δt)2
This subtraction may come as a surprise, but it reflects the fact that time is fundamentally different from the three spatial dimensions. Indeed, we notice that time is different in our everyday experience: you can steer a car so that it points north, east, south, or west, but you can't steer it to point to the past or the future (unless it's a DeLorean).
[Technical note: (Δx)2 + (Δy)2 + (Δz)2 - (Δt)2 may be negative, so some people prefer to reverse all the positive/negative signs and talk about -(Δx)2 - (Δy)2 - (Δz)2 + (Δt)2 instead.]
Based on this formula, when we calculate a "shortest" path through space time, we want to minimize (Δx)2 + (Δy)2 + (Δz)2 - (Δt)2 along the segments of the path. This means that we want to use less space when possible (smaller Δx, Δy, Δz), but more time when possible (larger Δt), since the square of time is subtracted rather than added. With this slightly strange geometry in mind, let's sketch out the shape of spacetime near earth. We've seen from experiments that clocks at lower heights from the earth's surface show less time passed than clocks higher up; loosely speaking, there's less time closer to the earth's surface. We can represent this by again drawing height on the vertical axis and time on the horizontal axis, and drawing gaps near the earth's surface to represent the smaller amount of time measured by clocks closer to the earth's surface:
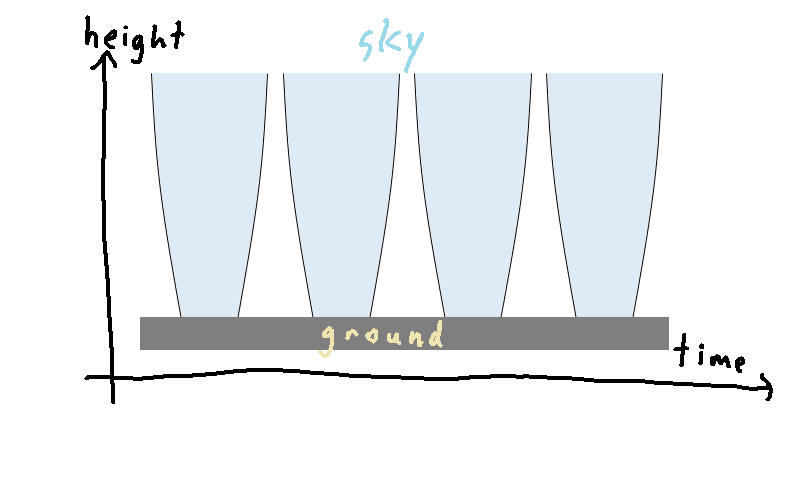
(Although the diagram above represents only two of the four spacetime dimensions, nothing much actually happens in the two omitted dimensions; the height and the time are the only interesting ones. For more mathematical detail about this shape in all four spacetime dimensions, see the Schwarzschild solution to Einstein's equations.)
Finally, let's draw the trajectory of the rising and falling ball on the diagram:
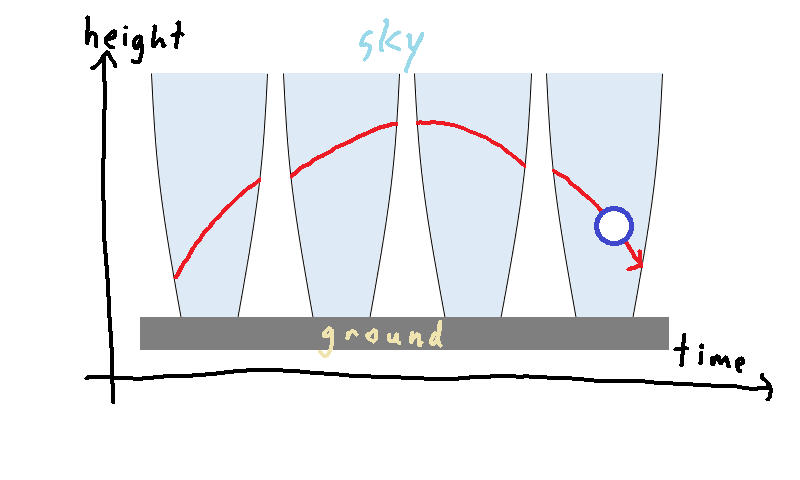
Notice that the ball rises to a height where it experiences more time than it would have if it had stayed low. This is similar to an airplane's great circle route traveling north to a latitude with less east-west distance, but with a sort of reversed logic. In the familiar geometry of the earth's surface, the airplane heads north to decrease the east-west distance it travels through. In the unfamiliar geometry of space-time, the flying ball goes up to increase the time it travels through. This results in the ball flying up and then falling back down, rather than flying down and falling back up. In other words, the particular shape and geometry of spacetime makes things fall down rather than up.
Except for the embedded videos and images already explicitly attributed to other other authors,
the images and text in this document were made by Chris Hawblitzel
and are licensed under a Creative Commons Attribution 4.0 International License.
.svg){kind=link}
